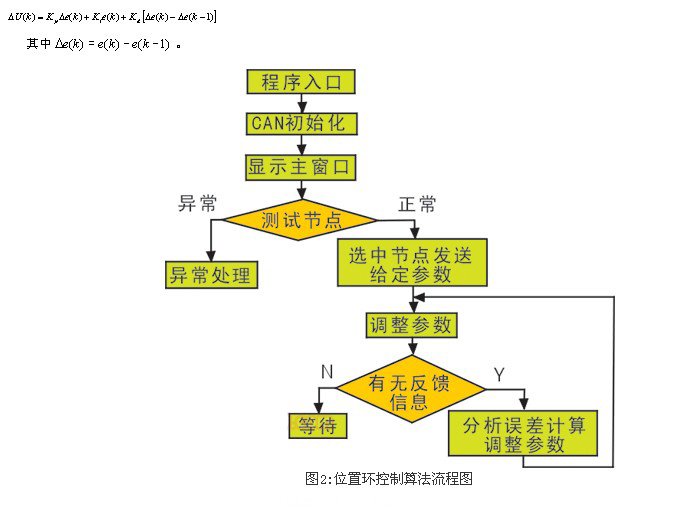
位置環pid控制算法

　　在數字pid調節控制系統中，引入積分環節的目的是為了消除靜差，提高精度，但在過程的開始、結束或大幅增加設定值時，會產生積分積累，引起系統較大的超調，甚至震蕩，這對于伺服電機的運行來說是不利的。為減小電機在運行過程中積分校正對控制系統動態性能的影響，采用積分分離pid控制正當其時，當電機的實階位置與期望位置的誤差小于一定位置時，再恢復積分校正環節，以便消除系統的穩態誤差。

　　積分分離pid控制算法需設定積分分離閥ε，當|e（k）|》ε時，即偏差值較大時，采用pd控制，以保證伺服電機位置控制精度。

　　離散化pid控制算式是：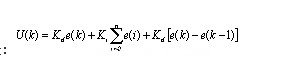

    其中，k為采樣序號，k=0，1，2…;

　　kp、ki、kd分別表示比例，積分、微分系數。在實際中，若執行機構需要的是控制量的增量，根據遞堆原理可得增量式pid控制算式為：

控制系統參數的整定

　　主控微機向控制卡發送pid參數，看給定的參數是否符合控制系統的要求，該過程需用參數整定實現。參數整定得主要任務是確定kp、ki、kd及采樣周期t，比例系數kp增大，使伺服驅動系統的動作靈敏，響應加快，而過大會引起振蕩，調節時間加長;積分系數ki增大，能消除系統穩態誤差，但穩定性下降;微分控制可以改善動態特性，是超調量減少，調整時間縮短。通常的方法有擴充臨界比例度法和擴充響應曲線法，以及歸一參數整定方法。這幾種方法源于使用齊格勒-尼柯爾斯（ziegler-nichols規則），通常可認為交流伺服系統的模型為一階段有延遲環節的模型（帶滯后的一階環節）：

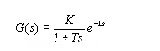
    式中的一階段響應特征參數k、l、和t可以由圖3所示的s型響應曲線提取出來。求取這些參數對實際系統并不困難，可以通過對系統進行階躍輸入激勵，得到響應曲線，再根據曲線求出其特征參數。于是可由ziegler-nichols整定規則得到：

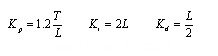
　　數字系統中采樣周期的選擇與系統的穩定性密切相關。一方面要滿足香農定理，即ωs≥2ωmax實際系統輸入及反饋的最大頻率ωmax難以測定，另一方面采樣周期并沒有一個精確的計算公式，只能根據工程應用按經驗規則選取，對于電機控制系統，要求較短時間采樣周期，通常為幾十毫秒。#p#分頁標題#e#

　　對于交流位置伺服控制系統而言，采用基于pc機的開發平臺，用常規的pid調節器進行控制，只要參數整定適當，加之系統的機械精度（運動軸、齒輪、電機絲杠傳動化）控制在一定誤差范圍內，電氣控制精度（編碼器脈沖）就可得到提高，魯棒性強，可以在很多場合達到較高精度位置控制的要求。